在职业能力测验数量关系中行程问题往往是最难理解最难解决的，然而在近几年的各类型考试中数量关系考察的难度有所下降。那么接下来给大家介绍一下行程问题中相遇问题如何通过比例法快速的解决，从而来帮助大家提升数量关系的做题速度。下面通过几道习题来帮助大家理解比例法解行程问题。

　　例1：甲乙两车分别从A、B两地同时出发相向而行，如果两车按原定速度行驶，5小时相遇;如果甲车比计划每小时多行1千米，乙车比计划每小时少行5千米，则7小时相遇。问A、B两地的距离为多少千米?

　　A.70B.80C.90D.120

　　答案：A。解析：这道题目是相遇问题的基础题，就这道题而言可以有2种解题思路。第一种整除法：根据题干信息我们知道A、B两地的距离是一定的，所以两种情况下路程不变，根据路程=速度×时间，所以路程既能够被5整除又能够被7整除，结合选项能够满足题意的只有A项。第二种就是今天想要和大家分享的比例法：我们知道路程是一定的，速度与时间成反比，而相遇问题，相遇的路程和=速度和×时间，两次速度有了变化，我们可以根据速度的变化来求解路程的实际量，两次情况时间之比为5：7，则速度之比为7：5，速度和比计划少了4千米，而速度少了两份，一份对应的实际量是2千米，则计划的速度和为14千米，所求路程为70千米。

　　接下来我们再看一道进阶题目，利用比例法解题。

　　例2：甲以每小时10千米的速度从家去单位，当他走了一半路程时发现把合同落在了家里，于是他以每小时15千米的速度回家去取，同时家人同样以每小时15千米的速度去送。他们相遇后甲仍以每小时15千米的速度赶往单位，结果比平时晚到5分钟。求甲的家到单位的距离为多少千米?

　　A.2.5B.4C.5D.7.5

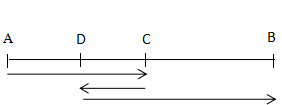
　　答案：C。解析：根据题干信息我们可以画出甲的行程图(如下)，题干中我们知道若路程是一定的，速度变化了，时间比原来晚到了5分钟，我们可以优先想到比例法来解这道题目，若走相同路程，速度之比为2：3;时间之比则为3：2;由此我们可以知道甲按照原来的速度行走AC用了3份时间，则行走AB用6份时间;而甲实际所走的路程所用的时间为：甲开始走AC用3份的时间，从D—C再从C—D速度变化了用2份的时间，故从C—B用了2份的时间，所以实际甲用了7份的时间，与原来相比多用了一份的时间，多用了5分钟，故走完全程原来所用的实际时间为30分钟，路程为10×0.5=5千米。答案为C。

　　通过以上的两道行程的题目讲解希望能够对学员在解决行程问题上有所帮助，在以后做数量行程中相遇问题时能够拿到分数